Why Gravity Affects Light
The Mystery of Mass and why Gravity affects Light
Why read on? In this section we prove that light is affected by a gravitational field even though light is massless.
It puzzled scientists for a long time that mass was use as a fundamental calculating factor in these two different cases. So much so that the two cases lead scientists to talk about two different forms of mass. The mass used in F = ma is called the inertial mass. The mass in F = Gm₁m₂/r² is called the gravitational mass. Experiments have been conducted from about 1900 until now to see if there is any measurable difference between inertial and gravitational mass. The details are quite interesting so there are references at the end if you are interested. The results from experiments by Eötvös in 1908 where he established that they were the same to an accuracy of 2 x 10‾⁹. In 2017 the MICROSCOPE experiment provided an accuracy of 10‾¹⁵.
Why the fuss? Does it matter? Well yes it does. It leads to the Principle of Equivalence (next section) which was the guide, always in the background, when Eistein developed his General Theory of Relativity. Hence to black holes, theories of the universe and here on Earth enabling the accuracy of GPS.
Stage 2. The Principle of Equivalence.
Here we will use the idea of a “thought experiment”. These are a useful tool in physics theory as they allow analysis of a situation which could not be realised in practice. It relates to seeing mass in its relation to inertia and comparing this with seeing mass in its relation to gravity.
Consider the following thought experiment. On the left (a) is a spaceship without windows accelerating with an acceleration of 9.8 ms‾². The spaceship is totally quiet and vibration free. On the right (b) is a sealed laboratory on Earth where the acceleration due to gravity is 9.8 ms‾².
To make this argument we will:
Stage 1 – talk about the strange nature of mass.
Stage 2 – explain the Principle of Equivalence.
Stage 3 – show how it follows that light is affected by gravity.
Stage 4 – give some experimental evidence to confirm the fact that light is so affected.
Stage 1. The Strange Nature of Mass.
Mass, measured in kg, a mystery – surely not? In order to explain the problem let’s look at situations where mass comes into some fundamental physics.
First, Newton’s second law of motion.
F = ma
What does this tell us about mass? If we write the equation as a = F/m then we can see that, for a given force, a greater mass will make the acceleration smaller. We think of mass as a measure of how difficult it is for a force to get something accelerating. We say mass is a measure of inertia.
The inertia is the same everywhere. A given force acting on any particular mass will produce the same acceleration, whether on the Earth, the Moon or in outer space. The difference between mass and weight is important. Mass is the same everywhere, but weight is a force and is the pull of gravity between the mass and other masses. Weight should be measured in newtons and will vary according to the location of other masses. This brings us to the second fundamental law involving mass.
Newton’s law of universal gravitation.
F = Gm₁m₂/r²
This law says that two masses m₁ and m₂ will attract one another with a force F when their centres are a distance r apart. G is the universal constant of gravitation which is the same everywhere in the universe. (Subject to current debate!)
But what is mass doing here? It is being used to calculate the force of gravitational attraction. Nothing to do with inertia.
So here we have the mystery. Mass is a physical quantity that is used in two utterly different phenomena, inertia and gravity. No other physical quantity does this.
Let’s try a counter argument to the fact that mass is the ONLY property that behaves this way. What about temperature, for example? You will know that the temperature of a gas affects the average kinetic energy of the atoms and molecules. There is a precise law that relates the temperature to the average KE. The temperature of a gas is involved in Gay Lussac’s law which relates the temperature to the pressure at a fixed volume. So here we have another property, temperature, involved in two different things and so mass is not alone? But this is not the case. The pressure of a gas is caused by the molecular movement. It is possible to derive Gay Lussac’s law from the relationship between KE and temperature. Newton’s second law and the Newton’s law of gravity have absolutely no relationship whatever – one cannot be derived from the other.
It puzzled scientists for a long time that mass was use as a fundamental calculating factor in these two different cases. So much so that the two cases lead scientists to talk about two different forms of mass. The mass used in F = ma is called the inertial mass. The mass in F = Gm₁m₂/r² is called the gravitational mass. Experiments have been conducted from about 1900 until now to see if there is any measurable difference between inertial and gravitational mass. The details are quite interesting so there are references at the end if you are interested. The results from experiments by Eötvös in 1908 where he established that they were the same to an accuracy of 2 x 10‾⁹. In 2017 the MICROSCOPE experiment provided an accuracy of 10‾¹⁵.
Why the fuss? Does it matter? Well yes it does. It leads to the Principle of Equivalence (next section) which was the guide, always in the background, when Eistein developed his General Theory of Relativity. Hence to black holes, theories of the universe and here on Earth enabling the accuracy of GPS.
Stage 2. The Principle of Equivalence.
Here we will use the idea of a “thought experiment”. These are a useful tool in physics theory as they allow analysis of a situation which could not be realised in practice. It relates to seeing mass in its relation to inertia and comparing this with seeing mass in its relation to gravity.
Consider the following thought experiment. On the left (a) is a spaceship without windows accelerating with an acceleration of 9.8 ms‾². The spaceship is totally quiet and vibration free. On the right (b) is a sealed laboratory on Earth where the acceleration due to gravity is 9.8 ms‾².
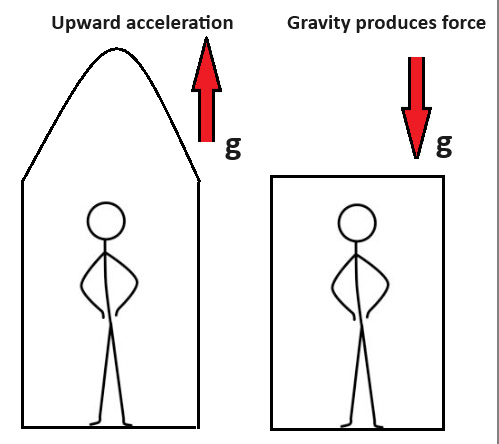
Let’s also suppose that the scientists in each have been quietly placed there while asleep and so have no idea whether they are in the spaceship or the lab. (Put aside practicalities – this a thought experiment). Can the scientists tell whether they are in the spaceship or the lab? They each have access to any equipment they want to call on.
Anything in the spaceship is caused by inertial forces as things are accelerating. In the lab it is gravity having the effects. So far no-one has found any method which could be used to differentiate, even in principle.
Aside. We do have to neglect the tiny difference in g between the floor and the roof of the lab. But this does not affect the principle. We could confine apparatus within an arbitrarily small vertical height! After all this is still a thought experiment.
If we cannot tell the difference, Eistein argued that at some deeper level the explanation must be the same. It was this thought that helped guide him when developing his General Theory of Relativity, although it is not possible to deduce the theory from this idea. It is more that the General Theory of Relativity is always consistent with this Principle of Equivalence.
Stage 3. Light is affected by gravity.
This what we are trying to prove. We do not expect light to be affected by gravity as it has no mass. If F = Gm₁m₂/r² and one of the masses is zero, then the force is zero. But from the Principle of Equivalence, we can immediately prove that light is affected by gravity provided we can prove that light bends inside something accelerating. So we start by looking at an accelerating rocket and showing that a light beam will bend.
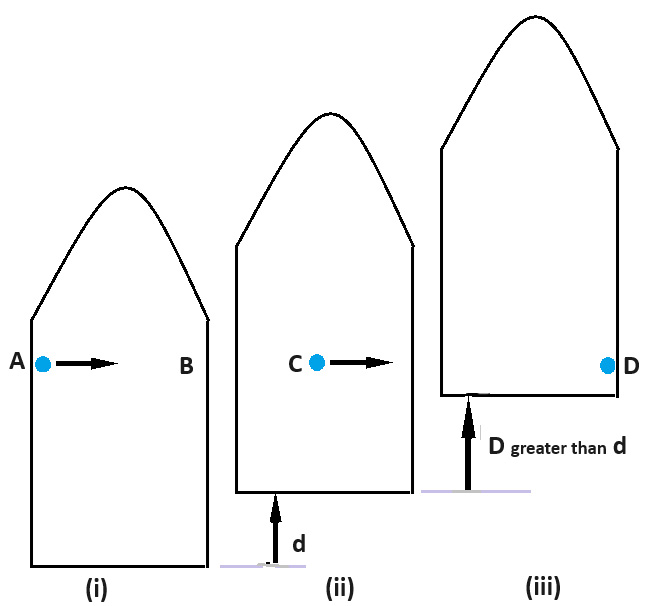
Figures (i), (ii) and (iii) show an imaginary spaceship accelerating upwards. The time interval between each picture is the same, but because of the acceleration the spaceship moves up more between Figure (ii) and (iii) than it does between (i) and (ii).
In Figure 1 a small laser at A fires a short pulse of light aimed at the opposite side of the spaceship towards B. This is another thought experiment so we can make the acceleration very large. We can suppose that by the time the light gets to the middle of the spaceship the rocket’s acceleration has left the beam behind and the short pulse is at C. If Figure (iii) the continuing acceleration means that the ships upward movement D is greater than before, so the beam hits the opposite side of the spaceship at D. An observer in the spaceship will therefore see the light pulse following a curved path, as shown below.
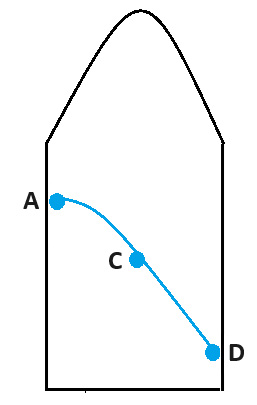
Here is the key! If we accept the Principle of Equivalence, it follows that light must also be bent in a gravitational field even though light itself is massless. This is what we set out to prove.
Stage 4. Experimental Evidence.
Light bending in a gravitational field can be observed in a total eclipse of the sun where stars become visible as the sun’s light is blocked by the moon. A particular star observed near the edge of the sun should not have been visible as it should actually have been hidden by the sun. The light from the star was, however, bent by the sun’s gravity so that it could be seen. The picture below shows how this worked.

In fact, with a bit of “handwaving” assuming the particle theory of light it is possible to predict this bending with Newton’s laws. An analysis using General Relativity predicts the answer for the bending to be exactly double that of the Newton value. Detailed measurements during an eclipse have shown that Einstein was correct. This remains one of the classic tests of the Theory of General Relativity.