Curious Case of the Garden Hosepipe
Any object will either stay put or carry on in a straight line unless some force acts on them. Objects thrown curve towards the Earth because of the Earth’s gravity. In deep space away from gravitational influences any object thrown would continue indefinitely in a straight line. This is a loose statement of Newton’s First Law of Motion.
So apart from the curve due to gravity water emerging from a hose pipe should initially set off in very nearly a straight line. But it doesn’t as the video below shows.
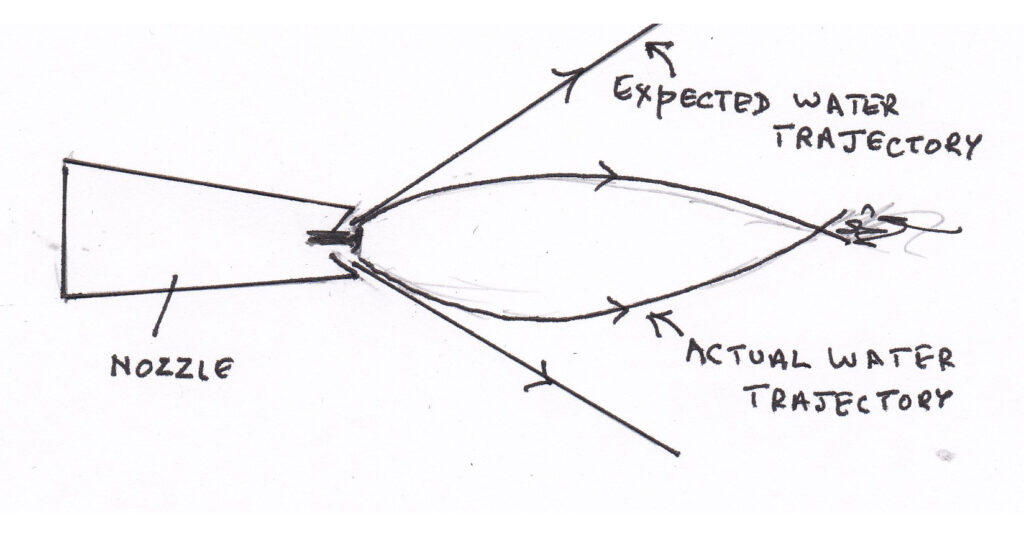
The water forms a curved bulb with air inside instead of emerging straight. The question is what force must have been acting on the water to cause this shape.
When the water emerges from the cone shaped nozzle, it would expand outwards, but this does not explain why it converges back towards itself. The sketch below shows this.
The logical explanation is that the pressure of the air should be lower inside the bulb. Milo and I made a water manometer. This is a U shape of plastic tubing partly filled with water. If you suck gently on one side the water levels become uneven showing the lower pressure.
When one end of the tube was inserted through the wall of the bulb, the manometer showed no effect. If there was a pressure difference it must be small.
The rest of the project became a bit theoretical working out what the pressure difference needed to be to form the bulb. The calculation is given below, but the result is that the pressure difference needed to maintain the bulb is very small. Too small in fact to be measured on a manometer. At least that failure is explained.
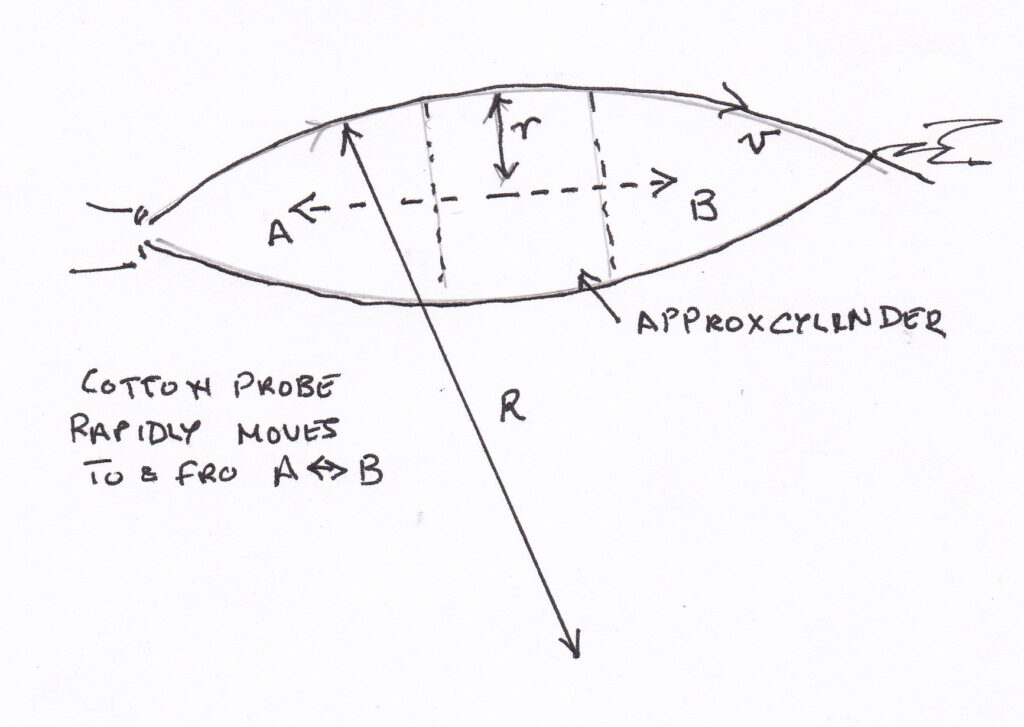
But we still did not know where this reduction in pressure was coming from. Milo decided to try to see how the air was moving, if at all, inside the bulb. He got a very thin but strong piece of wire and attached a piece of cotton thread 2cm long to the end. When this was poked into the bulb the cotton flicked to-and-fro very fast along the axis of the bulb. Unfortunately we took no video.
It seems therefore that the reduction in pressure is probably related to this rapid air motion. There is a bit more discussion on this at the end of the technical section. But we still don’t know why the water forms this bulb.
Calculating the Pressure Difference Needed
We took an image of the bulb so that this could be printed out and measured. A rule was against the bulb so that we could get estimates of the actual bulb size and curvature. Here is the picture.

To do the calculations the following data is needed:
- The radius “r” of the cross section of the bulb. This could be found directly from the print of the above photograph.
- The radius “R” of the curved wall of the bulb. The diagram below shows exactly what theis means. Again found from the photograph.
- The speed “v” of the water emerging from the nozzle. This had to be found by measuring the height “h” that the water would reach when projected vertically upwards.
- The thickness of the thin wall of the bulb “t”. To find this we also needed to measure the volume flow per second. This together with the geometry already measured could give the answer. This was done by collecting water volme “V” in a measuring bucket over a measured time “T”.
The measurements were as follows:
r = 0.04 m, R = 0.35 m h = 1.5 m V = 1.5 litres = .0015 cubic metres and t = 13 s
To find the speed we use the fact that the KE of any part of the stream must equal the PE at the top of the vertical fountain where the KE is zero.
So using mgh = mv2/2 we get that v = 5.5 m/s
As an approximation consider the central part of the bulb as a short cylinder. The radius ir and the wall thickness is t. As t is thin the area of the thin wall is 2πrt very nearly. Water is travelling at v m/s through this so the volume per second is 2πrtv. This must equal the measured volume of water per second i.e. V/T
So 2πrtv = V/T. We know all the values in this except t. Putting in the numbers gives t = .08mm. We take this as 0.1 mm since all of this is somewhat approximate. The idea is to get an order of magnitude.
Now to get the pressure difference.
Consider a small “patch” in surface of the bulb of area A, so having a volume At. The mass of material in this bulb = ρAt where ρ is the density of water. This mass is moving in a circle of radius R. The force needed to produce this motion is F = mv2/R which is also F = ρAtv2/R. The pressure difference needed is F/A so
Pressure difference = ρtv2/R
Putting in the numbers this gives 8.6 Pa.
This would support a column of water of just less than 1mm which is why the manometer failed to measure any reduction of pressure in the bulb.
So to sum up. We know that there is less pressure inside the bulb and it is this that keeps the water in the bulb moving in an approximately circular arc. We do not know why the pressure is less and think it must be something to do with the rapid to-and-fro air movements in the bulb. It is possible to see that as the water moves out initially from the nozzle just at the moment of switching on so expanding the air at this moment. But it cannot explain the continuing lower pressure where the air in bulb is essentially trapped. It is the curious case of the garden hosepipe.