Inertia of Energy - E = mc²
To prove Einstein’s famous equation we will:
Stage 1 – compare the usual view E = mc² with the idea of energy possessing inertia.
Stage 2 – consider and hopefully clarify the concept of binding energy.
Stage 3 – consider the experimental evidence for the idea that a photon possesses momentum.
Stage 4 – use the idea from stage 3 and some very basic physics to prove E = mc².
Stage 1. E = mc² and the Inertia of Energy.
In nuclear fission a nucleus of Uranium, with the help of a neutron, can split into two separate nuclei with a few extra neutrons as well. We don’t need to worry here about the precise details. If, however, we add up the masses of the uranium nucleus and neutron at the start and compare this with the total mass of all the bits after the fission we find that the mass before is slightly greater than the mass after. Mass appears to have been lost.
The difference in mass is called the mass defect and this is usually interpreted as mass being turned into energy showing up as the kinetic energy of the “fission fragments”. In turn this KE is passed by collisions to the general atoms and molecules around. That is, it appears as heat and light.
The amount of energy E is found from Einstein’s famous equation E= mc², where c is the speed of light.
There is, however, a different way of looking at this. Consider a box with a spring lying unstretched at the bottom. Its mass is measured on very sensitive equipment. Now the spring is stretched across the box as in the second diagram and its mass measured again. There would be a slight increase in mass. (There is, unfortunately, no possible apparatus that could do this with sufficient sensitivity so again this is a “thought experiment”.) We interpret this by saying that the extra energy in the box possesses inertia given by m = E/ c².
This equation m= E/ c² then defines the inertia of the amount of energy E. Using an ordinary spring you could make a rough guess of E and so work out m knowing that c = 3 x 10⁸ m/s. You find that this is far too small for any balance to measure.
In fission the change in mass is much larger compared to the mass of the nuclei.
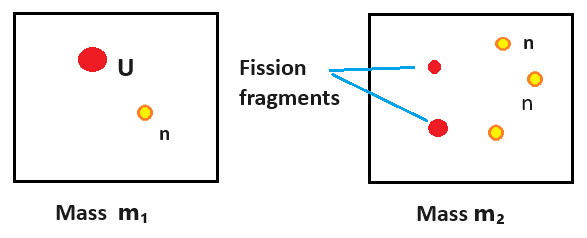
That is the mass defect m₁ – m₂ is more significant compared to m₁. This why nuclear reactions produce much more energy. You can find numerical examples on the web showing this. The decrease of energy of the nuclei released as KE means that the inertia of that energy is no longer locked up in the nuclei, so the mass decreases by m₁ – m₂ = (Energy release)/ c².
Stage 2. Binding Energy
This is a term that can easily cause confusion. Suppose you have a system of particles all separate and you want to get them to stick together. If these were ball bearings you could use Bostik or Araldite and glue them. If the particles are components of a nucleus what can take the place of the glue. The answer is decidedly NOT energy. If you add energy you will stir things up not get them to stick together. To get things to stick you need to REMOVE energy. In doing so you are removing inertia so a nucleus held together will have a smaller mass than that of all the particles separately. It is hard to understand this if you stick entirely thinking of mass turning into energy. The idea of inertia of energy is more convincing.
So binding energy is not the energy to get the nuclear particles to stick but is the energy you need to pull them all apart. Or it is the energy you need to remove to get them to stick together.
Stage 3. Photon Momentum
Light can be thought of as particles called photons. A photon has momentum equal to its energy E/c where c, as usual is the speed of light. This was confirmed experimentally by Compton in 1923 using the study of X photons being scattered by electrons. Crudely, he fired X rays at block of was and saw how the X rays were scattered. This and some careful measurements of the wavelengths scattered with some maths gave the confirmation that:
Photon momentum p = E/c.
Sounds simple but it was not really, and the work won him the Nobel prize a few years later.
Stage 4. Proof of E= mc²
To do this we need the extra bit of extra information above for the value of the photon momentum, then it is plain sailing.
Here is the usual thought experiment. Consider an isolated long box with something at A that can emit a single photon. It can be absorbed at the other end at B.

Here is the gist of the argument. When a photon is emitted from A there will be a recoil and the box will move to the left. The box will continue to move while the photon is in transit. It will stop when the photon is absorbed at B. During this time the box will have moved a little to the left. It would seem, therefore, that the centre of mass has moved. But this is impossible if the box is isolated and there are no external forces. The explanation is that the inertia of the photon energy is now at B – rather than A – and so this shifts the centre of mass back to its original position. The maths of this argument gets us to required result as you can see below.
We suppose that the mass of the whole box is M. When the photon is emitted, the whole box will recoil with a speed V. The conservation of momentum says that the momentum of the whole box to the left is equal to the momentum of the photon to the right. So
MV = p = E/c ——-(1)
The recoil movement stops when the photon reaches B and is absorbed. The time t taken for the photon to travel is L/c where L is the length of the box.
During this time the box will have recoiled to the left by a distance
d = Vt = VL/c. ——–(2)
This is now the key. If the box is isolated its centre of mass cannot move. But the box as a whole has moved to the left. It is only possible for the centre of mass to be in the same place if some mass has moved to the right. This must be the inertia of the photon.
To keep the centre of mass in the same place
Mass moving left x distance moved left = mass moving right x distance moved right.
So Md = mL ————(3)
where m is the inertia of the photon that moves right the whole length of the box.
Put the value of d from (2) into (3)
MVL/c = mL
And now put the value of MV from (1) into this last equation
(E/c)(L/c) = mL => EL/c² = mL
Cancel the L and E/ c² = m
Finally, E = m/c²