The Twin Paradox or Why we can Journey to the Future
Stage 1 – considers and argues the fact that the speed of light is an invariant – always the same however measured.
Stage 2 – The twin paradox. The reasoning here show that if one from a pair of twins travels sufficiently fast and then returns, the twin staying on Earth will have aged more. The ‘space’ twin has travelled into the future.
Stage1. The invariance of the speed of light.
Special relativity has two fundamental principles.
- The speed of light is an invariant.
- The laws of physics must be the same for all observers moving at a steady speed in relation to one another. Put more simply: F=ma is going to work irrespective of whether I am in a laboratory, or in train passing by at a steady speed. If we compare the numbers for the results of two relatively moving observers, they may well be different, but the laws those numbers obey will be the same. This may seem obvious but has far reaching consequences when analysed in detail.
Why do we believe that the speed of light is an invariant and what exactly does that mean?
I am driving at 20mph towards a car that is travelling at 60 mph. The relative speed of approach is 80 mph. If a different car starts off just ahead of me and travels at 60 mph and I follow at 20 mph then the relative speed away from me is just 40 mph.
Similarly with light I might expect that if I was in a fast rocket moving with half the speed of light towards the source of light, I would expect to measure the speed of light passing me as 1.5 times the value if the rocket were still. If I was moving away at half light-speed then I might expect the speed of light to be measured as just 0.5 the value were I stationary.
But light does not obey these rules of relative velocity. In all circumstances the speed of light I would measure would be the same 3 x 10⁸ m/s. This is so whether I am moving, or the source of light is moving, light-speed is the same in all these circumstances. It is an invariant.
What is the evidence for this? One major piece of evidence arises from Maxwell’s equations which are the basic laws of electromagnetism. In this theory there are two fundamental constants of nature. ₀ which is called the permeability of free space and relates the strength of magnetic fields to the moving charges or currents that produce them. The other is ε₀ which relates the strength of electric field to the charges producing them. Maxwell’s equations predict the existence of electro-magnetic waves and also predicts their speed as:
₀ε₀)
The derivation of this only involves considering the magnetic and electric fields in free space. It does NOT involve anything to do with whether the source of waves or the observer looking at them are moving. The speed of light is a property of free space with a value involving just these two fundamental constants of nature.
There is also much experimental evidence which you can look up. The most famous is the Michaelson-Morely experiment from the late 1800s. More recently there is evidence from the fragments of supernovae which have a whole range of speeds. If the speed of light emitted by these fragments was affected by their speed, then the images of these fragments would arrive at the earth at different times. This is not the case. They arrive at the same time showing the speed of travel has not been affected by the speed of the source.
Aside. You may say that this cannot be right as a substance like glass slows light down and causes refraction. If you look at the glass on an atomic scale the individual atoms scatter light. So light does not have an uninterrupted passage through the glass. The light travels at its invariant speed between scatterings. A somewhat involved calculation shows that the net effect of this scattering is the same as if the light had travelled through the glass at a slower speed.
An extreme case of this is light from the centre of the sun where the bulk of the nuclear reaction occur. The light from the surface of the sun takes just over 8 minutes to reach the Earth. The scattering in the centre of the sun is such that light can take up to about 170,000 years to et to the sun’s surface. One might say the refractive index at the centre of the sun is rather large!
So let’s take it that Maxwell and the considerable evidence from experiment are correct and see where that gets us.
Stage 2. The Twin Paradox
The consequences of Special Relativity are very numerous, but we shall take just one. The twin paradox is one that has caused more discussion and argument than many others – particularly in the middle of the twentieth century – so that has been chosen to discuss here.
Briefly: There are twins Elissa and Margot. Margo is a bit “stay at home” and so refuses to go with Elissa on a journey which travels for 20 months at high speed into deep space and then turns round and comes back again in another 20 months. To both twins on Elissa’s return, they find that 50 months has passed by on Earth. Had Elissa have travelled faster still, then the difference in the times would have been even greater.
This should not really be called a paradox as in theory it could happen. What prevents it is not having rockets fast enough and the inability of the human body to stand the accelerations needed on take-off, return and turning round at half-time.
The argument to show the truth of the difference in time is very much based on the invariance of the speed of light, and we need a bit of a preamble before we get into the argument proper. This involves a “space-time” diagram as shown below.
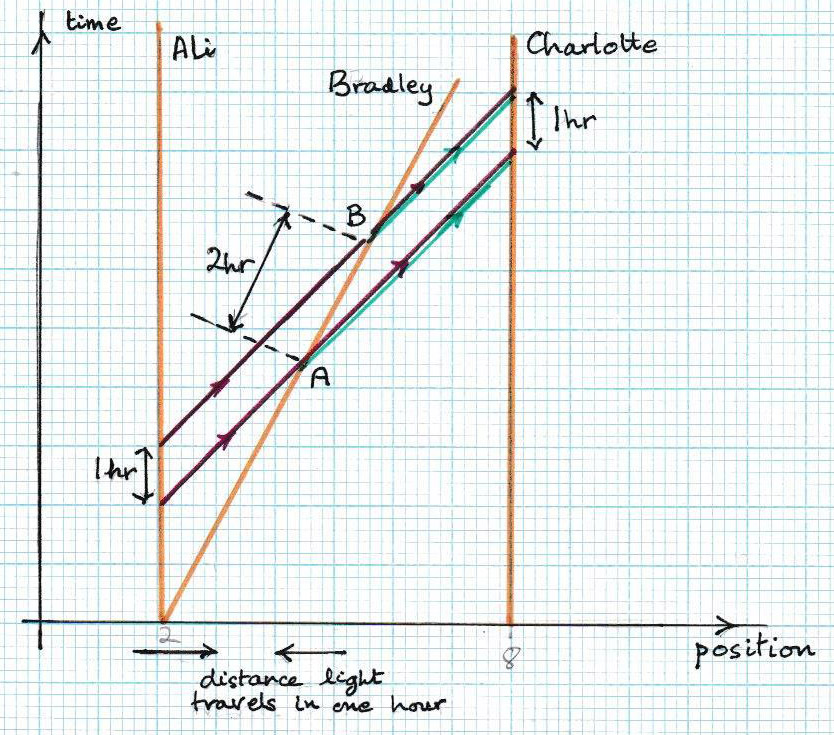
The vertical axis is time in hours. The horizontal axis represents position. The units on the horizontal axis are very large. Each square being the distance light travels in an hour. We will call these units l-hours.
At t = 0 Ali is at 2 l-hours from the origin. So he is at t = 1, 2, 3 hours. So Ali occupies a stationary position 2 l-lours from the origin. Similarly, Charlotte is stationary at 8 l-hours from the origin. Bradley, on the other hand, at t = 0 is at 2 l=lours and at about t = 1.8 he is at 3 l-hours. So he is moving fast along the x axis.
Now let’s see how Ali, Bradley and Charlotte may communicate. He only possibility is to use electromagnetic waves – lets use light. Suppose Ali sends a red-brown light signal towards Bradley (and Charlotte) at t = 2 hours. [Don’t forget this is a space-time diagram – the vertical axis is time. Ali, Bradley and Charlotte are all somewhere on the x axis at all times.]
Notice we have chosen units on the axes so that light travels one unit along that axis while the time on the vertical axis also goes up by one unit. So the light is represented by a line at 45 degrees.
When Bradley gets this signal, he sends a green flash also in Charlotte’s direction. Since the speed of light is an invariant the fact the Bradley is emitting the light as he moves makes no difference to the light. So the green flash accompanies the red flash and they both arrive at Charlotte at the same time.
Then Ali sends a second flash red-brown flash 1 hour later. This will arrive at Bradley more than one hour after the first arrived as he has travelled away further in the I hour so the light has further to go to reach him. Let’s suppose his speed is such that on his watch the time between the two red flashes is 2 hours. (In actual fact to achieve this Bradley must move at 3/5 of the speed of light, but we don’t need the actual speed for this argument).
So with this speed Bradley would get the flashes spaced twice the time the Ali emitted them. Now look at the green flashes from Bradley. These are space 2 hours apart but received by Charlotte 1 hour apart. So when the two people are moving towards one another with this speed the time interval between flashes is halved.
This is an example of a general rule. If two observers are moving apart with a speed V, then flashes emitted by one with be received by the other at a longer interval. Say it is k times longer. Then if they approach with this speed V the flashes will be shorter when received by a factor 1/k. In the rest of this argument, we will stick to double when moving apart and half when approaching.
Using this information, we can now come back to the twin paradox. Here is a space-time diagram for the situation where Elissa sends signals back to Margot at 5-month intervals. You can see that Elissa is moving away for the first 20 months on her clock, and then turns round and spends 20 months coming back.
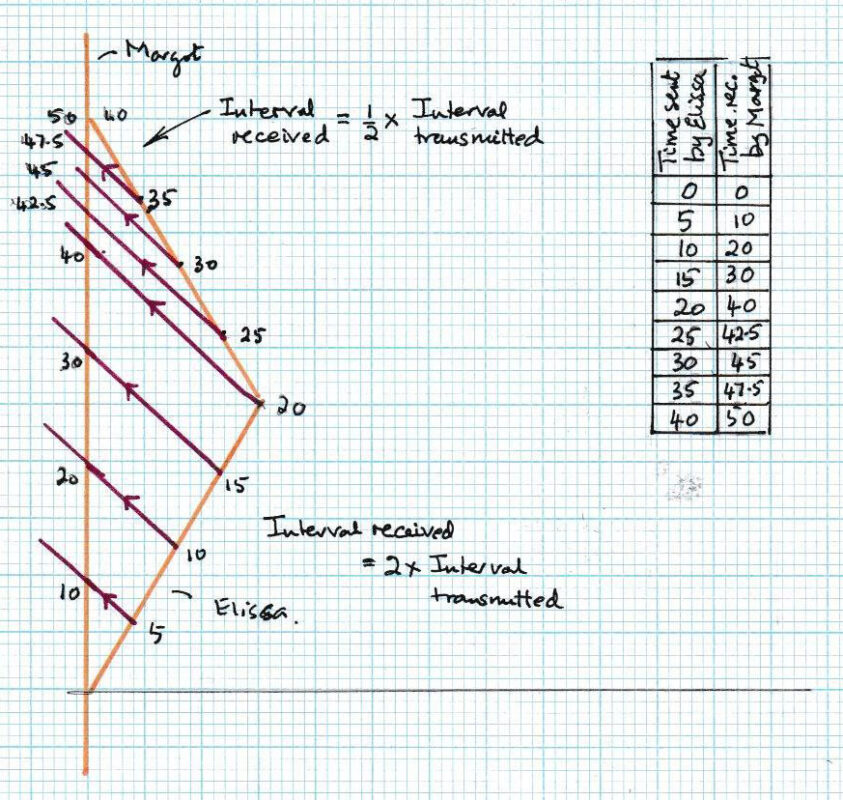
You can see that during the first 20 months Elissa sends 4 signals each 5 months apart. These are received at double spacing so 10 months apart. The times that Margot receives these are marked on the vertical axis. He remaining signals sent at 5-month intervals are received at half that amount, that is 2.5 month intervals. Again, the times are marked on the axis. You will see that, according to Margot, Elissa arrives back 50 months after she departed. But from Elissa’s point of view only 40 months have passed. In these different times each will have breathed the number of normal times per day and Margot will have done what she would normally do in 50 months and Elissa has dome what she would normally do in 40. Elissa has travelled into the future!
Let’s see if this gives the same result (as it should) if we look at it from the point of view of Margot send 5-monthly messages.
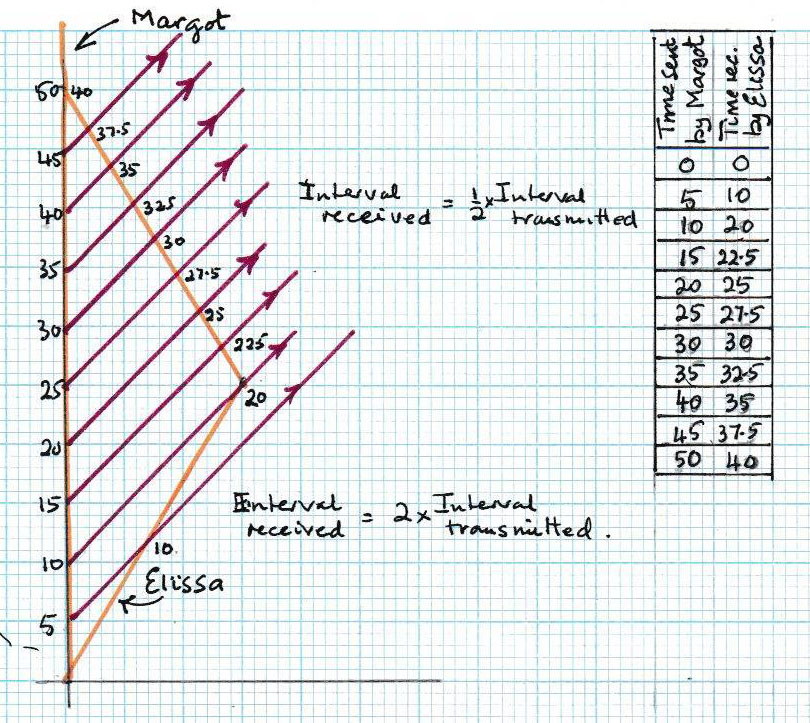
Here just two message are received by Elissa before she turns round, at 10 months and 20 months as they are receives with double the 5-month separation of emission. All the others are received while Elissa is moving back and are received at 2.5 month intervals. The time of receipt is marked on the diagram and also listed in the table.
Again, the consistent result is seen. Margot has sent messages ove a 50 month period but these been received by Elissa over a 40 month period. Either way Elissa has moved into the future.
And that is how it actually is!
There are many consequences of Special Relativity in developing physics theory. But there is also one everyday use. GPS. The accuracy of GPS depends on adjustments that need to be made because of the speed of the satellites. GPS adjustments (in the opposite direction!) also need to be made as the satellites orbit in a gravitational field which involves General Relativity. Although Special and General Relativity give opposing corrections, they are not equal, so to make GPS work with accuracy needs the predictions of both theories.